Kruskal Wallis test in R-One-way ANOVA Alternative
Kruskal Wallis test in R, Kruskal Wallis test is one of the frequently used methods in nonparametric statistics for analyzing data in one-way classification.
It is equivalent to a one-way analysis of variance in parametric methods.
When we test the identicalness of the k population from which the independent samples have been drawn. There is no restriction of sample sizes.
Decision Trees in R » Classification & Regression »
Assumptions
Mainly Kruskal Wallis test is based on the following assumptions.
- The observations are independent within and between samples.
- The variable under study is continuous
- The populations are identical in respect to the median.
Principal component analysis (PCA) in R »
Hypothesis
Ho: All the populations are identical
H1: At least one pair of the population do not have the same median.
The test statistic is approximately distributed as chi-square with (k-1) degrees of freedom. , subject to the condition n should be large or at least n should not be less than 5.
Kruskal Wallis test in R
Load Package
library(tidyverse) library(ggpubr) library(rstatix)
Getting Data
set.seed(345) PlantGrowth %>% sample_n_by(group, size = 1)
Output:-
weight group
1 5.18 ctrl
2 4.41 trt1
3 5.26 trt2
Ordering the group is really important when you are doing Duncan’s multiple comparison tests.
Repeated Measures of ANOVA in R Complete Tutorial »
PlantGrowth <- PlantGrowth %>%
reorder_levels(group, order = c("ctrl", "trt1", "trt2"))
Summary
PlantGrowth %>% group_by(group) %>% get_summary_stats(weight, type = "common")
Output:-
group variable n min max median iqr mean sd se ci 1 ctrl weight 10 4.17 6.11 5.155 0.743 5.032 0.583 0.184 0.417 2 trt1 weight 10 3.59 6.03 4.550 0.662 4.661 0.794 0.251 0.568 3 trt2 weight 10 4.92 6.31 5.435 0.467 5.526 0.443 0.140 0.317
Visualization
ggboxplot(PlantGrowth, x = "group", y = "weight", fill="group")

Based on the box plot, it evident that some difference exist between treatment 1 and treatment 2.
Kruskal Wallis Test
res.kruskal <- PlantGrowth %>% kruskal_test(weight ~ group) res.kruskal
Output:-
.y. n statistic df p method 1 weight 30 7.988229 2 0.0184 Kruskal-Wallis
Based on the p-value significant difference was observed between the group pairs.
Effect size
The effect size values normally interpreted as 0.01- < 0.06 (small effect), 0.06 – < 0.14 (moderate effect) and >= 0.14 (large effect).
PlantGrowth %>% kruskal_effsize(weight ~ group)
.y. n effsize method magnitude 1 weight 30 0.2217862 eta2[H] large
If effect size is large easily we can identify the significant differences based on small number of sample sizee.
Pairwise comparisons
Based on the Kruskal Wallis test we identified a significant difference, but we don’t which pair is significantly different. A pairwise comparison will help us to identify the significant pair.
Wilcoxon Signed Rank Test in R » an Overview »
res1<- PlantGrowth %>% dunn_test(weight ~ group, p.adjust.method = "bonferroni") res1
Output:-
.y. group1 group2 n1 n2 statistic p p.adj p.adj.signif 1 weight ctrl trt1 10 10 -1.117725 0.26368427 0.79105280 ns 2 weight ctrl trt2 10 10 1.689290 0.09116394 0.27349183 ns 3 weight trt1 trt2 10 10 2.807015 0.00500029 0.01500087 *
Based on the pairwise comparison significant difference was observed between Treatment and Traetment2.
res2 <- PlantGrowth %>%
wilcox_test(weight ~ group, p.adjust.method = "bonferroni")
res2
.y. group1 group2 n1 n2 statistic p p.adj p.adj.signif 1 weight ctrl trt1 10 10 67.5 0.199 0.597 ns 2 weight ctrl trt2 10 10 25.0 0.063 0.189 ns 3 weight trt1 trt2 10 10 16.0 0.009 0.027 *
Based on Wilcoxon test also significant difference was observed between treatment 1 and treatment 2.
Paired test for dichotomous data-McNemar’s test in R »
Visualization with p-values
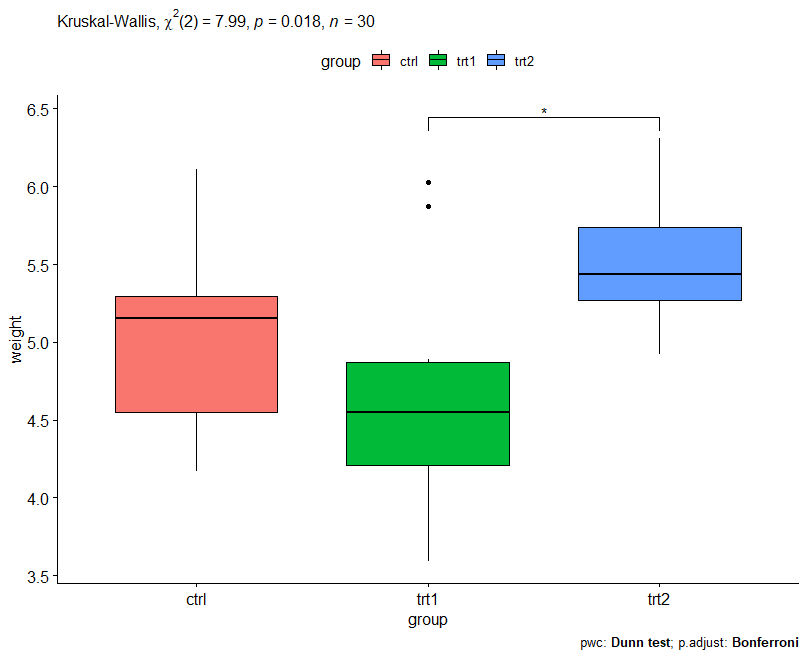
res1 <- res1 %>% add_xy_position(x = "group") ggboxplot(PlantGrowth, x = "group", y = "weight") + stat_pvalue_manual(res1, hide.ns = TRUE) + labs( subtitle = get_test_label(res.kruskal, detailed = TRUE), caption = get_pwc_label(res1))
Conclusion
Kruskal-Wallis test is an alternative to the one-way ANOVA when there are more than two groups to compare.
When ANOVA assumptions are not met It’s recommended.