How to Find Optimal Clusters in R?
How to Find Optimal Clusters in R, K-means clustering is one of the most widely used clustering techniques in machine learning.
With the K-means clustering technique, each observation in a dataset is assigned to one of K clusters.
The ultimate goal is to have K clusters in which the observations are relatively similar to one another within each cluster and considerably dissimilar from one another within different clusters.
Best Books on Data Science with Python – Data Science Tutorials
The first stage in k-means clustering is to decide on a value for K or the number of clusters we want to group the observations into.
The elbow method is one of the most popular approaches to choosing a value for K.
It entails plotting the total inside the sum of squares on the y-axis and the number of clusters on the x-axis to locate the plot’s “elbow” or bend.
The best number of clusters to utilize in the k-means clustering algorithm is indicated by the location on the x-axis where the “elbow” occurs.
Filter Using Multiple Conditions in R – Data Science Tutorials
The elbow method in R is demonstrated in the example that follows.
How to Find Optimal Clusters in R
We’ll use the USArrests dataset from R for this example, which includes the proportion of the population residing in urban areas in each state, or UrbanPop, as well as the number of murder, assault, and rape arrests made per 100,000 citizens in each state of the United States in 1973.
The dataset may be loaded using the code below, which also demonstrates how to delete rows with blank values and scale each variable in the dataset to have a mean and standard deviation of 0 and 1, respectively.
How to handle Imbalanced Data? – Data Science Tutorials
Now let’s load the data
df <- USArrests
Then we can remove rows with missing values
df <- na.omit(df)
As you know before clustering we need to scale the data frame. Scale each variable to have a mean of 0 and sd of 1.
5 Free Books to Learn Statistics For Data Science – Data Science Tutorials
df <- scale(df)
Let’s see the first six rows of the dataset
head(df)
Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
We’ll use the fviz_nbclust() function from the factoextra package to make a plot of the number of clusters vs. the total inside the sum of squares in order to determine the ideal number of clusters to use in the k-means algorithm.
How to do Conditional Mutate in R? – Data Science Tutorials
library(cluster) library(factoextra)
Plot the number of clusters relative to the total within the sum of squares
fviz_nbclust(df, kmeans, method = "wss")

At k = 4 clusters, it appears like there are an “elbow” or bends in the plot. The sum of the total of the squares starts to level out at this point.
This indicates that using four clusters is the ideal amount to employ when using the k-means method.
Although employing more clusters might result in a lower sum of squares, we would probably be overfitting the training data, which would cause the k-means algorithm to perform worse on the testing data.
Add new calculated variables to a data frame and drop all existing variables (datasciencetut.com)
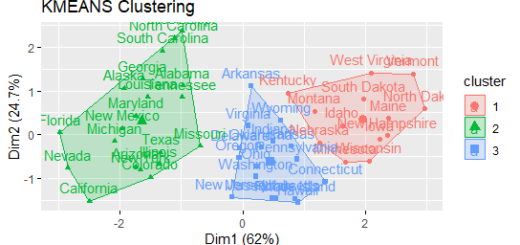
We can now run k-means clustering on the dataset using the kmeans() function from the cluster package and the recommended value of k of 4.
We can make this example reproducible
set.seed(1234)
Now perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)
Let’s view the output
km
K-means clustering with 4 clusters of sizes 13, 13, 8, 16 Cluster means: Murder Assault UrbanPop Rape 1 0.6950701 1.0394414 0.7226370 1.27693964 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 1.4118898 0.8743346 -0.8145211 0.01927104 4 -0.4894375 -0.3826001 0.5758298 -0.26165379 Clustering vector: Alabama Alaska Arizona Arkansas California 3 1 1 3 1 Colorado Connecticut Delaware Florida Georgia 1 4 4 1 3 Hawaii Idaho Illinois Indiana Iowa 4 2 1 4 2 Kansas Kentucky Louisiana Maine Maryland 4 2 3 2 1 Massachusetts Michigan Minnesota Mississippi Missouri 4 1 2 3 1 Montana Nebraska Nevada New Hampshire New Jersey 2 2 1 2 4 New Mexico New York North Carolina North Dakota Ohio 1 1 3 2 4 Oklahoma Oregon Pennsylvania Rhode Island South Carolina 4 4 4 4 3 South Dakota Tennessee Texas Utah Vermont 2 3 1 4 2 Virginia Washington West Virginia Wisconsin Wyoming 4 4 2 2 4 Within cluster sum of squares by cluster: [1] 19.922437 11.952463 8.316061 16.212213 (between_SS / total_SS = 71.2 %) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" [6] "betweenss" "size" "iter" "ifault"
Additionally, we can add each state’s cluster assignments to the initial dataset.
How to compare variances in R – Data Science Tutorials
Now add cluster assignment to the original data
finaldata <- cbind(USArrests, cluster = km$cluster) head(finaldata)
Murder Assault UrbanPop Rape cluster Alabama 13.2 236 58 21.2 3 Alaska 10.0 263 48 44.5 1 Arizona 8.1 294 80 31.0 1 Arkansas 8.8 190 50 19.5 3 California 9.0 276 91 40.6 1 Colorado 7.9 204 78 38.7 1
There are four clusters in which each observation from the first data frame has been sorted.