How to Calculate Cross-Correlation in R, The degree of resemblance between a time series and a lagged version of another time series is measured using cross-correlation.

In another way, it can tell us whether one-time series is a leading signal for another.

Cross-correlation is used in different areas like economics, business, Biology, etc…

Kendall’s Rank Correlation in R-Correlation Test »

Some of the common examples are given below.

1) The consumer confidence index (CCI) is regarded as a leading indicator of a country’s gross domestic product (GDP).

2) Marketing spend is sometimes regarded as a leading indicator of a company’s future revenue.

3) The total amount of pollution in the water is thought to be a leading indicator of the population of a particular turtle species.

In this tutorial, we are going to describe how to measure the cross-correlation between two time series in R.

Cross-Correlation in R

Let’s create a business example suppose the company spends on marketing and the revenue gained in that period.

#create data

Intraclass Correlation Coefficient in R-Quick Guide »

Spend <- c(5, 3, 6, 5, 8, 9, 10, 17, 12, 11, 10, 9)
Income <- c(25, 29, 22, 34, 22, 28, 29, 31, 34, 45, 45, 40)

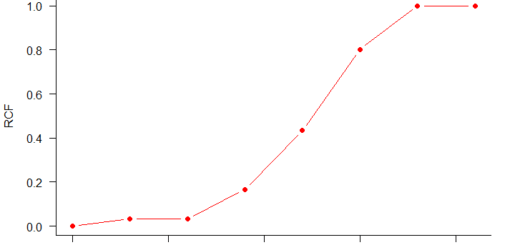
We can calculate the cross-correlation for every lag between the two-time series by using the ccf() function as follows:

measure cross-correlation

ccf(Spend, Income)

The above plot contains the correlation between the two-time series at various lags.

Obviously, numbers are more important, to get the original correlation values, we can make use of the print function.

How to Calculate Partial Correlation coefficient in R-Quick Guide »

print cross-correlation values

print(ccf(Spend, Income))

Autocorrelations of series ‘X’, by lag
    -7     -6     -5     -4     -3     -2     -1      0      1      2      3      4      5      6      7
-0.298 -0.137  0.094  0.475  0.677  0.730  0.607  0.340  0.222 -0.040 -0.226 -0.112 -0.333 -0.228 -0.273

Inference

The cross-correlation at lag 0 is 0.340

The cross-correlation at lag 1 is 0.222

The cross-correlation at lag 2 is -0.040

And so on.

Point Biserial Correlation in R-Quick Guide »