Random Forest in R
Random Forest in R, Random forest developed by an aggregating tree and this can be used for classification and regression. One of the major advantages is its avoids overfitting.
The random forest can deal with a large number of features and it helps to identify the important attributes.
The random forest contains two user-friendly parameters ntree and mtry.
ntree- ntree by default is 500 trees.
mtry- variables randomly samples as candidates at each split.
Random Forest Steps
1. Draw ntree bootstrap samples.
2. For each bootstrap, grow an un-pruned tree by choosing the best split based on a random sample of mtry predictors at each node
3. Predict new data using majority votes for classification and average for regression based on ntree trees.
Load Library
library(randomForest) library(datasets) library(caret)
Getting Data
data<-iris str(data)
The datasets contain 150 observations and 5 variables. Species considered as response variables. Species variable should be a factor variable.
data$Species <- as.factor(data$Species) table(data$Species)
setosa versicolor virginica 50 50 50
From the above results, we can identify that our data set is balanced.
Data Partition
Lets start with random seed so the outcome will be repeatable and store train and test data.
set.seed(222) ind <- sample(2, nrow(data), replace = TRUE, prob = c(0.7, 0.3)) train <- data[ind==1,] test <- data[ind==2,]
106 observations in train data set and 44 observatons in test data.
Random Forest in R
rf <- randomForest(Species~., data=train, proximity=TRUE) print(rf) Call: randomForest(formula = Species ~ ., data = train) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 2 OOB estimate of error rate: 2.83%
Confusion matrix:
setosa versicolor virginica class.error setosa 35 0 0 0.00000000 versicolor 0 35 1 0.02777778 virginica 0 2 33 0.05714286
Out of bag error is 2.83%, so the train data set model accuracy is around 97%.
Ntree is 500 and mtry is 2
Prediction & Confusion Matrix – train data
p1 <- predict(rf, train) confusionMatrix(p1, train$ Species)
Confusion Matrix and Statistics
Reference Prediction setosa versicolor virginica setosa 35 0 0 versicolor 0 36 0 virginica 0 0 35 Overall Statistics Accuracy : 1 95% CI : (0.9658, 1) No Information Rate : 0.3396 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 1 Mcnemar's Test P-Value : NA Statistics by Class: Class: setosa Class: versicolor Class: virginica Sensitivity 1.0000 1.0000 1.0000 Specificity 1.0000 1.0000 1.0000 Pos Pred Value 1.0000 1.0000 1.0000 Neg Pred Value 1.0000 1.0000 1.0000 Prevalence 0.3302 0.3396 0.3302 Detection Rate 0.3302 0.3396 0.3302 Detection Prevalence 0.3302 0.3396 0.3302 Balanced Accuracy 1.0000 1.0000 1.0000
Train data accuracy is 100% that indicates all the values classified correctly.
Naive Bayes Classification in R
Prediction & Confusion Matrix – test data
p2 <- predict(rf, test) confusionMatrix(p2, test$ Species)
Confusion Matrix and Statistics Reference Prediction setosa versicolor virginica setosa 15 0 0 versicolor 0 11 1 virginica 0 3 14 Overall Statistics Accuracy : 0.9091 95% CI : (0.7833, 0.9747) No Information Rate : 0.3409 - P-Value [Acc > NIR] : 5.448e-15 Kappa : 0.8634 Mcnemar's Test P-Value : NA Statistics by Class: Class: setosa Class: versicolor Class: virginica Sensitivity 1.0000 0.7857 0.9333 Specificity 1.0000 0.9667 0.8966 Pos Pred Value 1.0000 0.9167 0.8235 Neg Pred Value 1.0000 0.9062 0.9630 Prevalence 0.3409 0.3182 0.3409 Detection Rate 0.3409 0.2500 0.3182 Detection Prevalence 0.3409 0.2727 0.3864 Balanced Accuracy 1.0000 0.8762 0.9149
Test data accuracy is 90%
Error rate of Random Forest
plot(rf)
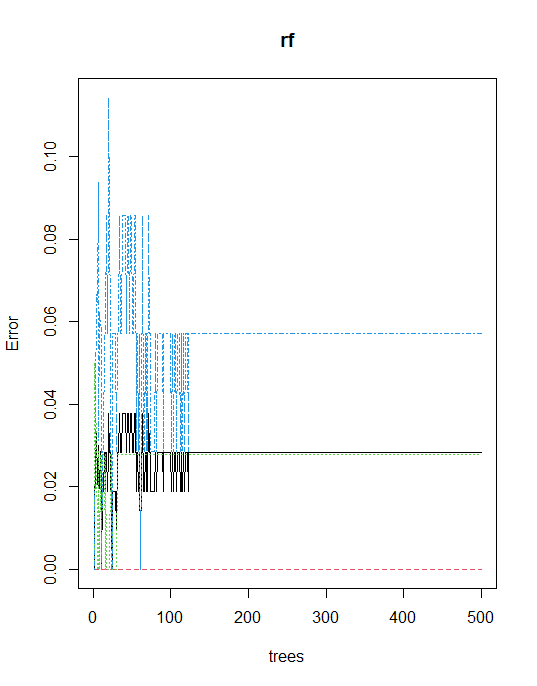
The model is predicted with high accuracy, with no need for further tuning. However, we can tune a number of trees and mtry basis below the function.
Tune mtry
t <- tuneRF(train[,-5], train[,5], stepFactor = 0.5, plot = TRUE, ntreeTry = 150, trace = TRUE, improve = 0.05)
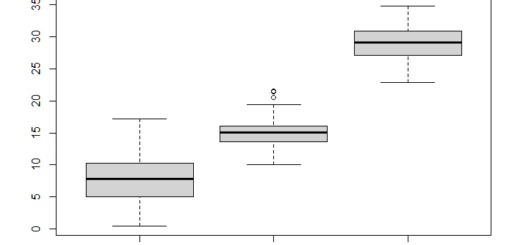
No. of nodes for the trees
hist(treesize(rf), main = "No. of Nodes for the Trees", col = "green") Variable Importance varImpPlot(rf, sort = T, n.var = 10, main = "Top 10 - Variable Importance") importance(rf) MeanDecreaseGini

Sepal.Length 7.170376 Sepal.Width 1.318423 Petal.Length 32.286286 Petal.Width 29.117348
Petal.Length is the most important attribute followed by Petal.Width.
Partial Dependence Plot
partialPlot(rf, train, Petal.Width, "setosa")
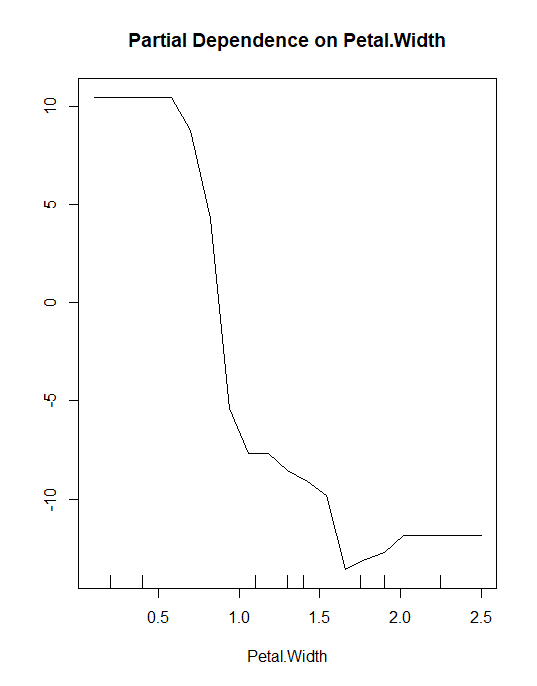
The inference should be, if the petal width is less than 1.5 then higher chances of classifying into Setosa class.
Multi-dimensional Scaling Plot of Proximity Matrix
Dimension plot also can create from random forest model.
MDSplot(rf, train$Species)
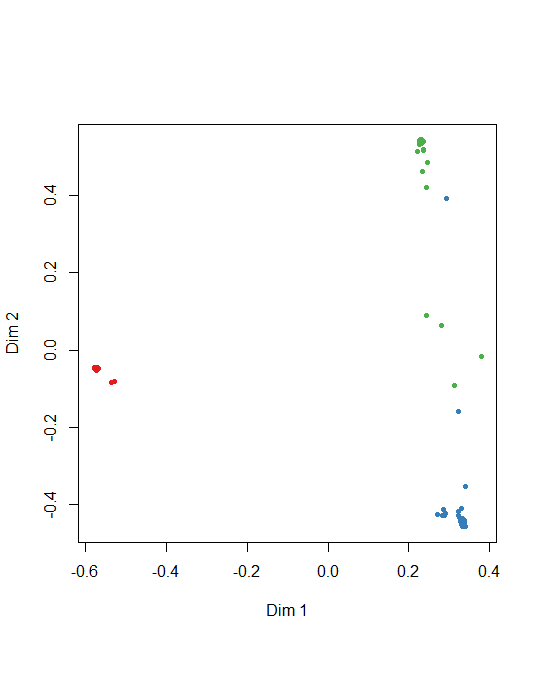




I worked through your tutorial with another dataset and experienced that the factor column needed to be the last column. Thanks for the tutorial
Yes, I took the response variable as the last column. Thanks for your reply…