How AI Turns Scores into Confident Decisions
How AI Turns Scores into Confident Decisions, When you take a multiple-choice test, you might feel 70% confident about answer A, 20% about answer B, and 10% about answer C.
Your brain intuitively converts these confidence levels into probabilities that sum to 100%. Similarly, AI systems like GPT do something comparable when deciding which word to generate next.
They use a mathematical function called softmax to transform raw scores—preferences that can be arbitrary—into valid probabilities.
What Is Softmax?
Softmax is a function that takes a list of numbers—called scores or logits—and converts them into probabilities that add up to 1.
Unlike simple normalization (dividing each score by the total), softmax emphasizes the larger scores, making the model’s choices more confident and decisive.
It ensures every output is positive and that the sum of all probabilities equals 100%.
How Does Softmax Work?
Mathematically, for each score ( z_i ), softmax computes:
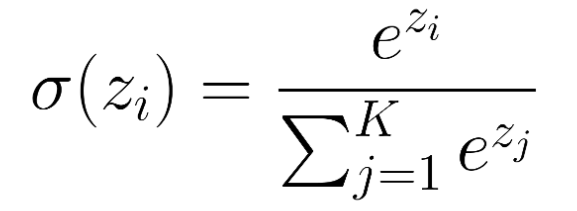
This means:
- Take the exponential of each score, amplifying differences.
- Sum all these exponentials.
- Divide each exponential by this sum to get a probability.
Example:
Suppose your scores are [2, 1, 0].
- e² ≈ 7.39, e¹ ≈ 2.72, and e⁰ = 1.
- sum: 7.39/11.11 ≈ 0.67, 2.72/11.11 ≈ 0.24, and 1/11.11 ≈ 0.09.
These probabilities sum precisely to 1, with the highest score receiving the largest share.
Why Use Exponentials?
Exponentials serve two key purposes:
- Guarantee positivity: Even negative scores become positive after exponentiation.
- Amplify differences: Slight score differences become more pronounced, leading to “winner-take-more” effects. For example, scores [3, 2, 1] produce a more decisive probability distribution than scores [6, 4, 2], even though their relative gaps are the same.
This amplification explains why language models can generate highly confident text when one word clearly fits better.
Controlling Confidence with Temperature
Softmax includes a temperature parameter ( T ), which adjusts how sharp or flat the distribution is:
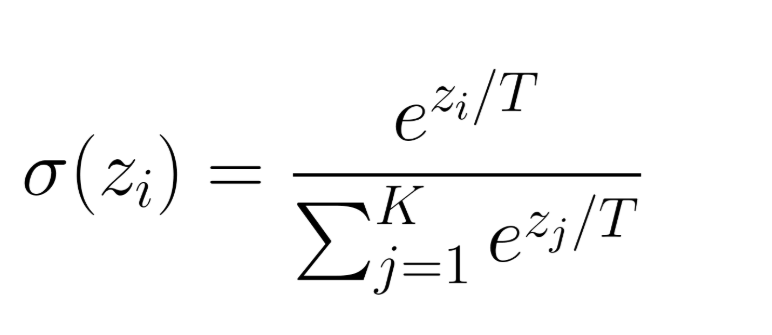
- Lower ( T ) (< 1): Sharpen the distribution, making top choices even more probable.
- Higher ( T ) (> 1): Flatten the distribution, increasing randomness and diversity.
Example with scores [4, 2, 1]:
| Temperature | Probabilities |
|---|---|
| 0.5 | [~0.98, ~0.02, ~0.00] (very sharp) |
| 1.0 | ~0.84, ~0.11, ~0.04 |
| 2.0 | [~0.63, ~0.23, ~0.14] (more diverse) |
Adjusting temperature allows AI to produce more predictable or more creative outputs.
Softmax in Action: Language Models
In models like GPT, softmax appears at the final step of word prediction:
- The model processes your input through numerous layers, generating a raw score for every word in its vocabulary (often 50,000+ words).
- These scores reflect the model’s preferences but aren’t probabilities yet.
- Softmax converts these scores into a probability distribution, where words with higher scores get higher probabilities.
- The model then samples from this distribution to select the next word.
Example:
Given the phrase “The weather today is very,” the model might score potential next words:
- “hot” (4.2)
- “cold” (3.8)
- “nice” (2.1)
- “rainy” (1.7)
- “windy” (0.9)
Softmax transforms these into probabilities:
- “hot”: 52%
- “cold”: 35%
- “nice”: 6%
- “rainy”: 4%
- “windy”: 2%
It then randomly chooses the next word based on these probabilities, balancing coherence with variety.
Why Not Just Normalize?
A common misconception is to normalize scores by dividing each by their sum. However, this approach fails with negative scores (which can produce invalid, negative probabilities).
For example, scores [4, -1, 2, 0] normalized linearly become [0.80, -0.20, 0.40, 0.00], which is invalid.
Softmax solves this elegantly by exponentiating scores—ensuring all probabilities are positive—and emphasizing differences without negative values.
Applications Beyond Language
While often associated with language models, softmax is a fundamental component across machine learning:
- Image classification: Assigning probabilities to different labels.
- Recommendation systems: Ranking items by relevance.
- Multi-class prediction: Deciding among multiple categories, ensuring the probabilities sum to 1.
For binary decisions, simpler functions like sigmoid are used, but softmax is ideal when choosing among many options.
Computational Considerations
Calculating softmax for large vocabularies can lead to numerical issues due to very large exponentials. To stabilize calculations, subtract the maximum score from all scores before exponentiating:
Adjusted scores = z_i – max_j z_j
This preserves the relative differences while preventing overflow, ensuring accurate probability calculations.
What Softmax Reveals About AI Behavior
Understanding softmax helps explain AI behaviors:
- When models produce unexpected but coherent outputs, temperature settings may be allowing lower-probability words to occasionally win.
- Repetitive outputs can result from very low temperatures, making the highest-probability choices dominate.
Moreover, small improvements in raw scores can lead to significant changes in output quality because the exponential function magnifies even tiny score differences.
Final Thoughts
Softmax is a crucial bridge between raw computational scores and meaningful probabilities. By applying exponential weighting followed by normalization, it transforms competing preferences into clear, actionable probability distributions.
This process underpins the confident language generation we see in AI systems, enabling them to make informed and nuanced decisions across a wide array of tasks.