Cumulative Distribution Function Calculation (CDF)
Cumulative Distribution Function Calculation (CDF), The Cumulative Distribution Function (CDF) is a fundamental concept in statistics and probability theory that describes the likelihood of a continuous random variable (X) taking on a value less than or equal to a specific value (x).
Cumulative Distribution Function Calculation
This critical function enables us to understand the probability distribution of various real-world phenomena.
Examples of scenarios requiring the calculation of CDFs include:
- The probability that a person is 180 cm tall or shorter
- The probability that a household’s annual income is below $50,000
- The likelihood of completing a marathon in 4 hours or less
- The probability of temperatures dropping below freezing
The Simplified Process of CDF Calculation
For individuals who might feel overwhelmed by technical terminology, this article offers a straightforward, step-by-step explanation of how to calculate CDFs for datasets that follow a normal distribution—one of the most commonly assumed types of continuous probability distributions.
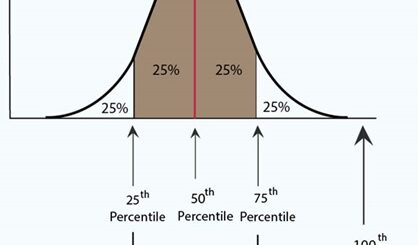
Visual Representation of Normal Distribution
A normal distribution, also known as a Gaussian distribution, is visually represented as a bell-shaped curve.
In this curve, values tend to cluster around the center, which is called the mean or average.
For instance, in a population where adult heights are measured, the majority of individuals are likely to fall within a specific range around the mean height.
As we move away from this center, values become increasingly rare.
The area under the curve up to a specific point represents the CDF.
For example, if we want to find the probability of (X) being less than or equal to 175 cm, the CDF is represented by the shaded area under the curve to the left of the point (X = 175).
Practical Example of CDF Calculation
To illustrate how to calculate the CDF, let’s consider a specific case: determining the probability that a randomly selected adult male is 175 cm tall or shorter (i.e., (P({Height} \175))).
To perform this calculation, we assume that the dataset represents measurements that follow a normal distribution, and we require the following parameters:
- Mean (average height): 170 cm
- Standard deviation (spread of the curve): 10 cm
The first step in our calculation is standardizing the target value (x = 175). Standardizing transforms the normal distribution into a standard normal distribution, which has a mean of 0 and a standard deviation of 1.
The standardized value, referred to as the z-score, can be calculated using the following formula:
z = {x – {mean}}/{{standard deviation}}
In our example, substituting our values gives us the z-score:
z = {175 – 170}/{10} = 0.5
Finding the CDF Using Tools
Calculating the CDF manually can be complex, which is why we typically rely on lookup tables or statistical software:
- Using a Z-Table: Although they may appear intimidating, Z-tables are user-friendly. Locate the row corresponding to the first decimal of your z-score (in this case, 0.5), then find the value in the corresponding column. For more precise z-scores (e.g., 0.51 or 0.54), refer to the column matching the second decimal.
- Coding Solutions: For those who prefer programming, you can easily calculate the cumulative probability with tools like Python’s SciPy library. Here’s a simple code snippet:
from scipy.stats import norm
cdf = norm.cdf(175, loc=170, scale=10)Regardless of the method you choose, both approaches yield a CDF value of approximately 0.6915, indicating that 69.15% of adult males are 175 cm tall or shorter.
In practical terms, this means if you randomly select an adult male from this population, there’s about a 69% probability he will be 175 cm or shorter.
Conclusion
This article provides a simplified overview of how to calculate Cumulative Distribution Functions (CDFs) for data that follow normal distributions.
Understanding this process and the various tools available to compute a CDF is invaluable in numerous real-world scenarios, making it easier to make informed decisions based on probability.
Arming yourself with this knowledge will enhance your statistical analysis and help you interpret data effectively in various contexts.
Whether you’re conducting research, analyzing data, or involved in decision-making processes, mastering CDF calculations can significantly boost your analytical capabilities.