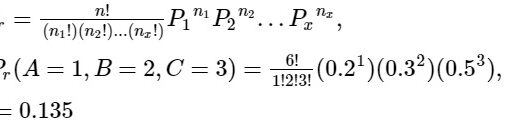How to perform Rolling Average in R
How to perform Rolling Average in R, A rolling average in time series analysis represents the average value over a predetermined number of prior periods.
Using the rollmean() function from the zoo package in R is the simplest approach to compute a rolling average:
library(dplyr) library(zoo)
Calculate the 3-day rolling average
df %>% mutate(rolling_avg = rollmean(values, k=3, fill=NA, align='right'))
For the column labeled values, this particular example computes a 3-day rolling average.
How to use this function is explained in the example that follows.
How to perform Rolling Average in R
Let’s say we have the following R data frame, which displays sales of a certain product over a period of 10 days:
Let’s create a data frame
df <- data.frame(day=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10), sales=c(215, 120, 114, 116, 217, 120, 112, 115, 114, 191))
df day sales 1 1 215 2 2 120 3 3 114 4 4 116 5 5 217 6 6 120 7 7 112 8 8 115 9 9 114 10 10 191
For each row of the data frame, we can add a new column called avg_sales3 that shows the rolling average of sales for the preceding three days:
library(dplyr) library(zoo)
Now calculate 3-day rolling average of sales
df %>% mutate(avg_sales3 = rollmean(sales, k=3, fill=NA, align='right'))
day sales avg_sales3 1 1 215 NA 2 2 120 NA 3 3 114 149.6667 4 4 116 116.6667 5 5 217 149.0000 6 6 120 151.0000 7 7 112 149.6667 8 8 115 115.6667 9 9 114 113.6667 10 10 191 140.0000
The quantity of prior periods used to generate the rolling average is controlled by the value of the k parameter in the rollmean() function.
The rolling average of the sales figure for the preceding three periods is displayed in the avg_sales3 column.
For instance, the first result of 149.6667 is determined as follows:
3-Day Moving Average is equal to 149.6667 (215 + 120 + 114) / 3.
The modify() function’s multiple rollmean() capabilities can be used to perform numerous rolling average calculations simultaneously.
The code below, for instance, demonstrates how to compute the 3-day and 4-day moving averages of sales:
ggplot2 scale in R (grammar for graphics) »