Gradient Boosting in R
Gradient Boosting in R, in this tutorial we are going to discuss extreme gradient boosting.
Why is eXtreme Gradient Boosting in R?
Popular in machine learning challenges.
Fast and accurate
Can handle missing values.
Is it requires numeric inputs?
Yes, eXtreme Gradient Boosting requires a numeric matrix for its input.
Sample Size calculation formula
Load Library
library(xgboost) library(magrittr) library(dplyr) library(Matrix)
Getting Data
data <- read.csv("D:/RStudio/NaiveClassifiaction/binary.csv", header = T)
str(data)'data.frame': 400 obs. of 4 variables: $ admit: int 0 1 1 1 0 1 1 0 1 0 ... $ gre : int 380 660 800 640 520 760 560 400 540 700 ... $ gpa : num 3.61 3.67 4 3.19 2.93 3 2.98 3.08 3.39 3.92 ... $ rank : int 3 3 1 4 4 2 1 2 3 2 ...
Data set contains total 400 obsevations and 4 variables. eXtreme Boosting requires numerical variable, so just convert rank data into factor variables.
data$rank <- as.factor(data$rank)
Partition data
Let’s partition the data sets into train data and test data.
set.seed(1234) ind <- sample(2, nrow(data), replace = T, prob = c(0.8, 0.2)) train <- data[ind==1,] test <- data[ind==2,]
Matrix Creation
In this case Rank variable is factor variable required hot encoding for the same. Based on hot encoding factor variables convert into dummy variable.
trainm <- sparse.model.matrix(admit ~ .-1, data = train) head(trainm)
6 x 6 sparse Matrix of class "dgCMatrix" gre gpa rank1 rank2 rank3 rank4 1 380 3.61 . . 1 . 2 660 3.67 . . 1 . 3 800 4.00 1 . . . 4 640 3.19 . . . 1 6 760 3.00 . 1 . . 7 560 2.98 1 . . .
train_label <- train[,"admit"] train_matrix <- xgb.DMatrix(data = as.matrix(trainm), label = train_label)
Now we converted train data sets in to necessary format., sameway we need to convert into test data also.
testm <- sparse.model.matrix(admit~.-1, data = test) test_label <- test[,"admit"] test_matrix <- xgb.DMatrix(data = as.matrix(testm), label = test_label)
Parameters
nc <- length(unique(train_label))
Basically 2 different classes in the train label datset
xgb_params <- list("objective" = "multi:softprob",
"eval_metric" = "mlogloss",
"num_class" = nc)
watchlist <- list(train = train_matrix, test = test_matrix)watch list will help us to identify the error in each iteration.
Naive Bayes Classification in R
Gradient Boosting in R
bst_model <- xgb.train(params = xgb_params, data = train_matrix, nrounds = 1000, watchlist = watchlist, eta = 0.001, max.depth = 3, gamma = 0, subsample = 1, colsample_bytree = 1, missing = NA, seed = 333)
##### xgb.Booster raw: 2.4 Mb call: xgb.train(params = xgb_params, data = train_matrix, nrounds = 1000, watchlist = watchlist, eta = 0.001, max.depth = 3, gamma = 0, subsample = 1, colsample_bytree = 1, missing = NA, seed = 333) params (as set within xgb.train): objective = "multi:softprob", eval_metric = "mlogloss", num_class = "2", eta = "0.001", ax_depth = "3", gamma = "0", subsample = "1", colsample_bytree = "1", missing = "NA", seed = 333", validate_parameters = "TRUE" xgb.attributes: niter callbacks: cb.print.evaluation(period = print_every_n) cb.evaluation.log() # of features: 6 niter: 1000 nfeatures : 6 evaluation_log: iter train_mlogloss test_mlogloss 1 0.692889 0.692974 2 0.692631 0.692793 --- 999 0.556583 0.625728 1000 0.556514 0.625710
Training & test error plot
e <- data.frame(bst_model$evaluation_log) plot(e$iter, e$train_mlogloss, col = 'blue') lines(e$iter, e$test_mlogloss, col = 'red')
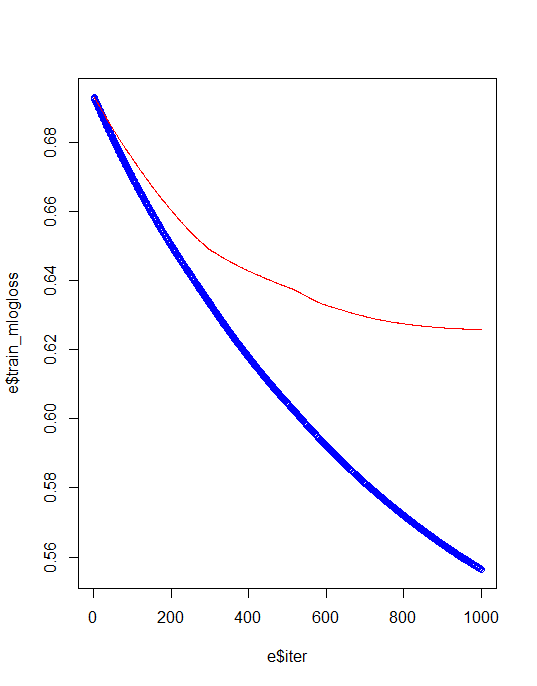
For avoiding overfiiting and best model creation we need to identify best iteration and eta values.
min(e$test_mlogloss) e[e$test_mlogloss == 0. 613294,]
We can rerun the model based on above values.
Gradient Boosting in R
bst_model <- xgb.train(params = xgb_params, data = train_matrix, nrounds = 2, watchlist = watchlist, eta = 0.613294, max.depth = 3, gamma = 0, subsample = 1, colsample_bytree = 1, missing = NA, seed = 333) Feature importance imp <- xgb.importance(colnames(train_matrix), model = bst_model) print(imp)
Feature Gain Cover Frequency 1: gpa 0.48632797 0.47722628 0.35714286 2: gre 0.23495920 0.32849509 0.42857143 3: rank1 0.23432569 0.17282919 0.14285714 4: rank2 0.04438714 0.02144944 0.07142857
xgb.plot.importance(imp)
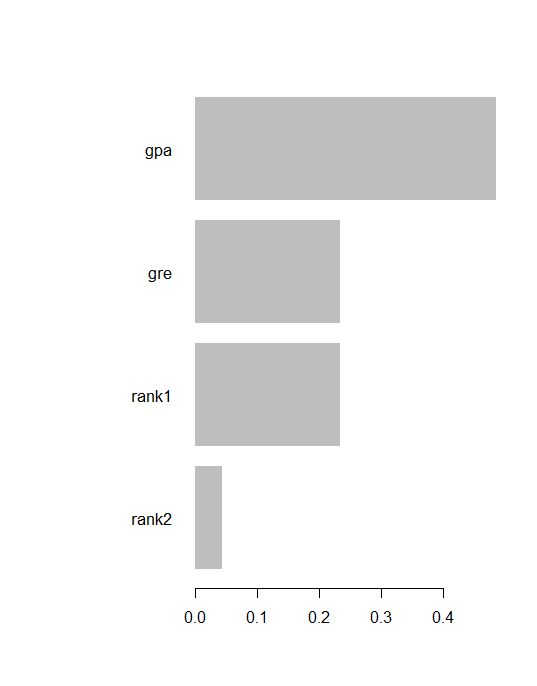
Prediction & confusion matrix
p <- predict(bst_model, newdata = test_matrix) Pred <- matrix(p, nrow = nc, ncol = length(p)/nc) %>% t() %>% data.frame() %>% mutate(label = test_label, max_prob = max.col(., "last")-1)
X1 X2 label max_prob 1 0.7780407 0.2219593 0 0 2 0.6580867 0.3419133 0 0 3 0.6111851 0.3888150 0 0 4 0.4440117 0.5559883 1 1 5 0.6111851 0.3888150 1 0 6 0.4345139 0.5654861 1 1 7 0.7780407 0.2219593 1 0 8 0.7780407 0.2219593 1 0 9 0.6580867 0.3419133 0 0 10 0.6580867 0.3419133 1 0 11 0.6159363 0.3840637 0 0 12 0.6580867 0.3419133 0 0 13 0.7780407 0.2219593 0 0 14 0.5099485 0.4900515 1 0 15 0.4440117 0.5559883 1 1 16 0.7780407 0.2219593 0 0 17 0.5099485 0.4900515 0 0 18 0.6111851 0.3888150 1 0 19 0.7780407 0.2219593 1 0 20 0.7780407 0.2219593 0 0 21 0.7780407 0.2219593 0 0 22 0.6580867 0.3419133 1 0 23 0.7780407 0.2219593 0 0 24 0.8379621 0.1620379 0 0 25 0.1789861 0.8210139 1 1 26 0.6111851 0.3888150 1 0 27 0.7780407 0.2219593 1 0 28 0.6111851 0.3888150 0 0 29 0.6580867 0.3419133 1 0 30 0.1789861 0.8210139 1 1 31 0.5099485 0.4900515 0 0 32 0.7780407 0.2219593 0 0 33 0.6111851 0.3888150 0 0 34 0.6111851 0.3888150 0 0 35 0.7581326 0.2418674 0 0 36 0.6111851 0.3888150 1 0 37 0.6111851 0.3888150 0 0 38 0.6580867 0.3419133 0 0 39 0.6111851 0.3888150 0 0 40 0.6111851 0.3888150 0 0 41 0.6580867 0.3419133 1 0 42 0.6111851 0.3888150 1 0 43 0.6111851 0.3888150 0 0 44 0.7780407 0.2219593 0 0 45 0.6111851 0.3888150 0 0 46 0.7780407 0.2219593 0 0 47 0.6111851 0.3888150 0 0 48 0.6580867 0.3419133 0 0 49 0.6111851 0.3888150 0 0 50 0.6111851 0.3888150 0 0 51 0.7780407 0.2219593 0 0 52 0.6111851 0.3888150 0 0 53 0.6111851 0.3888150 1 0 54 0.6159363 0.3840637 0 0 55 0.6111851 0.3888150 0 0 ........................ 75 0.5099485 0.4900515 0 0
0 indicates student not admitted and 1 indicates students admitted in the program.
table(Prediction = pred$max_prob, Actual = pred$label)
Actual Prediction 0 1 0 49 20 1 1 5
Conclusion
Based on this tutorial you can make use of eXtreme Gradient Boosting machine algorithm applications very easily, in this case model accuracy is around 72%.




Would you make the input file available. D:/RStudio/NaiveClassifiaction/binary.csv. Then we can run your example code. Thanks –
Now retrieving an image set.
The Art of Statistics
₹437.00 (as of July 3 23:00 GMT +07:00 - More infoProduct prices and availability are accurate as of the date/time indicated and are subject to change. Any price and availability information displayed on [relevant Amazon Site(s), as applicable] at the time of purchase will apply to the purchase of this product.)
Sure..Details you can avail from the below link
https://github.com/finnstats/finnstats
Now retrieving an image set.
The Art of Statistics
₹437.00 (as of July 3 23:00 GMT +07:00 - More infoProduct prices and availability are accurate as of the date/time indicated and are subject to change. Any price and availability information displayed on [relevant Amazon Site(s), as applicable] at the time of purchase will apply to the purchase of this product.)